account
The unexpected probability result confusing everyone

In this post, I will discuss how to get Samsung FRP tools for PC. These tools function beautifully in the FRP lock subject, and each of the tools listed below has unique capabilities and the capacity to overcome the FRP lock. So, to reset FRP, download FRP Unlock tool and follow our easy steps.
The unexpected probability result confusing everyone
#unexpected #probability #result #confusing
“Stand-up Maths”
Thanks to Dylan from Seattle for sending this amazing maths fact to me. You can see an archive of their ChatGPT conversation here:
Thanks to Grant from 3blue1brown for putting actual work aside and talking probabilities with me on a…
source
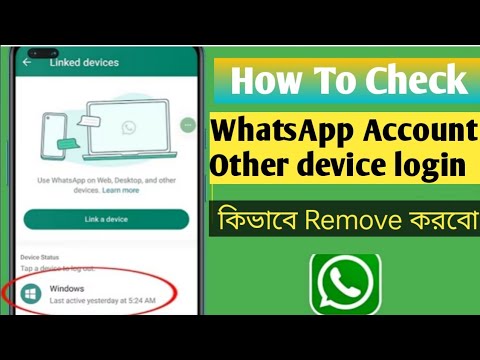
Another method for FRP
The only method to deactivate a Samsung account from a phone without a password is to contact Samsung to locate and delete the account. If you wish to begin the procedure on your Samsung phone, follow the comprehensive instructions below.
- Unlock your phone, then launch the Samsung phone settings app from the app drawer.
- Scroll down until you see "Cloud and Accounts." Also, on the next page, select the "Accounts" tab.
- Then, from the choices, select "Samsung Accounts" and then "My profile." When prompted to enter your email address and password on the account screen, select "Forgot your ID and Password." A popup will appear on the screen; from there, select your preferred browser.
- A prompted browser prompts you to enter your ID and password, as well as your email address. After that, Samsung will send you an email with a link to reset your password.
- Return to your Samsung account settings and select "Remove Account" from the top-right menu bar.
To see the full content, share this page by clicking one of the buttons below |


Let me know if this video contains your favourite ever Skylab the Dog cameo. I think it should.
I'm working on a system right now that replaces d20 rolls with 3d8 rolls to normalize roll distribution. For advantage, instead of rolling twice and taking the higher value, you roll 4d8 and take the THREE highest numbers. For double advantage, you take the best 3 of 5d8, and so on. For disadvantage we do the same, except we take the bottom 3 dice in each case.
Any idea how to calculate that?
Correction: 4:50 it's 2/3s of the max + 1/2 – 1/(6*max)
That's amazing!
Clearly taking the square root of the D36 cannot and is not equivalent to taking the maximum of two D6s. For one, as opposed to what is claimed in the video, it doesn't solve the resolution problem. If anything, it creates it! For the maximum of two D6s has 6 possible values, whereas the square root of D36 has… 36 possible values.
So what did you mean, @standupmaths? Did you want to say that the expected value is the same, or what?
One question: What's the dog's name?
Your deductions are non-provable. Y U ask?
Because you never defined R.
So does that mean that when rolling N dM with advantage,
u=E(x from 1 to M)[(x/M)^(1/N))]?
(u being expected value) I tested it with excel and it kinda works…
UPD: I discussed it with DeepSeek and it gave me another formula:
u=E(x from 1 to M)[x(((x/M)^N)-(((x-1)/M)^N))]
which one is more correct?
UPD2
According to Deepsek the formula is
u=E(x from 1 to M)[x(((a/M)^N)-(((a-1)/M)^N))]
with
a=x if rolling with advantage
a=M-x+1 if rolling with disadvantage
UPD3
About a disadvantage
Powering instead of rooting (is that the right word?) works!
u=E(x from 1 to M)[(x/M)^N]
The question remains though, if what DeepSeek gave me is more precise.
UPD4
I tested mine and AI formulas against the Monte-Carlo method. The AI's results differ far less from it. So it won, I guess…
Have you looked at the approach used to confirm a random number generator is actually random, with no bias? Asking for a friend :)
15:51 Why do you say "rounding up to the nearest whole number" when the table on the right clearly shows "rounding up to the nearest superior number" ??
12:23 You can see a dog in the background
14:55 You can see the dog again
Why is Matt holding one d6 under a radical and two more in a MAX function? Hear me out….
If we select random numbers from 0 to 1 our expected average will be 1/2. If we look at their square roots, we indeed get an expected average of 2/3. And if we look at two random numbers between 0 and 1, the average larger value is right at 2/3. The general content of the video is spot on.
However, if you roll a 6-sided die you will expect to get each of the 6 faces equally, so the expected average of the square roots would be (1 + sqrt(2) + sqrt(3) + 2 + sqrt(5) + sqrt(6))/6, which is about 1.81. But the maximum of two d6 rolls on average will be 161/36, about 4.47. I'm only an amateur mathematician, but I can see that these are two values which are not the same value.
(If we instead choose any random real number from 0 to 6 rather than just the faces of the dice, then the square root one averages to (I think) 2sqrt(6)/3 (about 1.63) while the max is 4 exactly.. One is going to be 2/3 of the largest number, the other is 2/3 of the square root of the largest number.)
So I'm confused by what the thumbnail is trying to say. It definitely works when the range of random numbers is 0 to 1, but look at f(x) = sqrt(x). At x = 0 f(x) = 0 and the slope is undefined/vertical. The outputs grow fast, but when we reach x = 1/4 the slope has dropped to 1. At x = 1 the slope is 1/2. (The slope at x = k is (2sqrt(k))^-1.) Past 1, the square roots grow too slowly to keep up with the max of two numbers in that range. So in the specific range 0 to 1 I can state that yes, the sqrt and the max are equivalent. Past 1, though, that stops happening. So this won't work with dice, unless they are numbered 0 to 1.
EDIT: At 14L00 he does mention this, but my note remains.
who else had to scroll back the video to see if the glass full of dice was empty all along?
so we're increasing the length of the interval by 2 each time, and not only that when we've got 2 numbers that are equal because they were both made by adding up exactly the same numbers! You know we lost somebody for a while to the drink, but now he's back and he's a bit worried about cracks in the earth but he's talking about g-d too! What we got so far are imposter numbers and if we booze these numbers they remain imposter numbers but they take on some properties of normal numbers, like they behave normally under equals. Now these imposter numbers usually need to be separated from normal numbers but its the negative roots that mean you can't really get rid of them, the usual way to determine if you're dealing with an imposter number is to examine its identity function, and if it isn't an imposter number it will only behave like one for the purposes of the examination – simple quantum physics really.
To be a little less un-rigorous: dx=y*dy+y*dy+dy*dy
Also it's chatGPT and chatGTP lol
def fastSQRTRandom():
n = rand()
m = rand()
return n if n > m else m
12:04 bro bought and glued together 216 dice
what's the calculator app on the phone ?
The randomiser on your phone is NOT random …and you can get more nuanced results, by using more dice.
come on, man, everyone knows that the singular of dice is douse
personal bookmark: 1:04
What a clickbait, the dices… i calculated it with dices and result was 11/216 that sqrt(x) > max (x1, x2). Which means that obvious choice is to chooe max(x1, x2). And then i thought no way that sqrt(x) is better choice and watched this video :)
Looking at the ball with the one "not a hexagon" gives me a wild amount of anxiety. I REALLY want to turn it so that I don't have to see the one weird side. I know there is a story behind it, but it still doesn't help my insanity.
Does that mean that you could do that with a d100 and 2d10
One die, not one dice. Die singular, dice plural.
0:22 what
ChatGTP lol
15:00 Using a single D36 instead of 2 D6's
(Nerd!)
im a little late to the party, but why you need a visual proof for n > 3? i mean the concept is clear and with the assumption of independence you get
P(max(X)<R)
= Π P(X_i < R)
= Π R
= R^n
= P(x<R)
edit: chat gpt proof at the end is actually correct, what a surprise.
i am pretty sure that is a standard math example in probability courses at university.
Matt, you should do a Delia Smith type show where you go through the basics of mathematics, just as Delia showed people on how to boil an egg.
12:22 dog spotted
14:56 dog returns for a second visit
quantum programming uses like between this range increase the probability of the solution occurring based on the program. So its basically test all those states at once but the values that return true flip the q-bit and at end vastly increase that chance picked at random would return. The probability of square root being max choice, maybe able to speed up a quantum algorithm. This video may improve quantum programming techniques. lol.
In the end matt used a single D36 to simulate 2 D6's, but I feel like the more fun task would be to figure out how to take normal die (like D6's) and figure out perfect ways to simulate bigger die.
For example, you should be able to perfectly simulate a D20 with 2 D(sqrt(20)) die!
I never understand these videos completely, but I always get enough out of them to turn my mind on for the rest of the day. I so love math! Just wish I was better at it.
You could resize an area of face to best represent the dice of probability.
Jim Carey whem did you go bald!?!
Does that mean sqrt(x) = Min(x1,x2) if you range is x>1 instead of [0,1]?
It's not surprising that chaptgpt answered correctly. Dylan guided chatGpt to the correct answer, effectively teaching it a new property. They didn't ask about random numbers in general, but used a specific function rand() found in many programming languages that have a specific domain. It is like asking chatGpt why the sky is blue? Or what is the color of Napoleon's white horse?
This is describing a process of identifying outputs of a function.
Knowing nothing else about the two functions (especially the inputs at any given time) results in a {number space} that are identical, or near identical.
The use-case for this is in reverse engineering a {black box function}
However; the use-case for each of these examples is obviously different.
And therefore; in order to determine the actual value {functional value}{or use-cases} you need to also know what the input values *are*.
Otherwise you could make the mistake in [objectively identifying] a function {or perhaps some mathematical observation about reality} as something it is definitely not.
Love the observation.
So it's impossible– nay, "there is a zero probability"– to pick a number at random with infinitely many decimal places…?